Cát tuyến là gì? Tính chất và cách vẽ đường cát tuyết
Cát tuyến là phần nội dung rất quan trọng trong Toán lớp 9 hay xuất hiện trong các bài kiểm tra, bài thi học kỳ. Vậy cát tuyến là gì? Tính chất và cách vẽ đường cát tuyến như nào? Hãy cùng chanhchua.com theo dõi trong bài viết này để nắm được phần kiến thức này chắc chắn để làm bài tập tốt nhất nhé!
Cát tuyến là gì?
Cát tuyến thực chất là một từ Hán Việt đã được dùng từ xưa. Trong đó, cát ở đây có nghĩa là đường cắt hoặc vết cắt, còn tuyến nghĩa là một đường thẳng. Do vậy, khi kết hợp với nhau thì từ cát tuyến có thể được hiểu đơn giản là một đường thẳng cắt các đường khác như: đường thẳng, đường cong, đường tròn, đường cao, đường trung tuyến,…
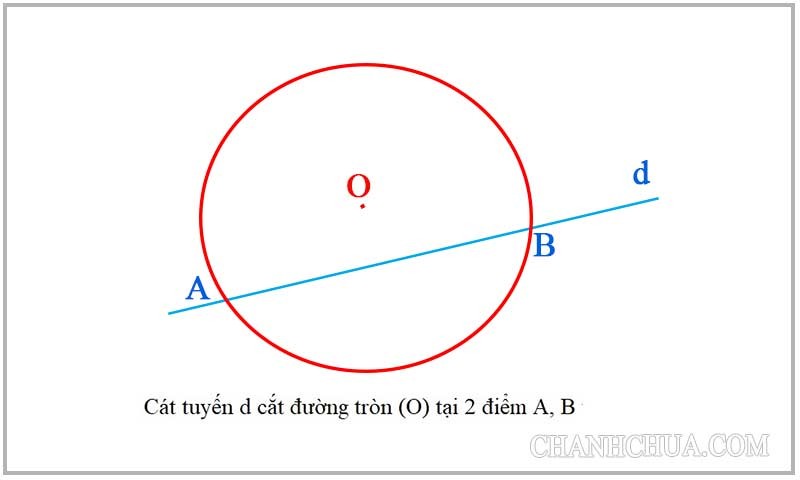
Theo định nghĩa cát tuyến trong sách giáo khoa Toán lớp 9 thì đây là một đường thẳng cắt với một đường thẳng khác. Cát tuyến của đường tròn chính là 1 đường thẳng bất kỳ cắt đường tròn đó tại hai điểm phân biệt. Cát tuyến của 2 đường thẳng chính là 1 đường thẳng cắt ngang với 2 đường thẳng nói trên. Trong một vài trường hợp đặc biệt thì đường cát tuyến có thể đi qua tâm của đường tròn.
Tính chất của đường cát tuyến
Sau khi tìm hiểu thông tin về khái niệm cát tuyến là gì ở bên trên, chúng ta sẽ cùng tìm hiểu đến tính chất của đường cát tuyến đó ở bên dưới đây.
Cho một đường tròn tâm O với hai đường thẳng AB và CD. Ta có:
- Nếu 2 đường thẳng AB và CD của một đường tròn giao nhau tại điểm M thì MA x MB = MC x MD. Đảo lại ta có, nếu 2 đường thẳng AB, CD cắt nhau tại M và có MA x MB = MC x MD thì bốn điểm A, B, C, D cùng thuộc trên một đường tròn.
- Nếu MC là tiếp tuyến và MA, MB là cát tuyến thì:
- MC = MA x MB = MO.MO – R.R
- Từ 1 điểm K nằm ở bên ngoài của đường tròn, ta lần lượt kẻ các tiếp tuyến KA, KB và cát tuyến KCD. H là trung điểm của CD thì 5 điểm gồm K, A, H, O, B sẽ cùng nằm trên 1 trung điểm.
- Vẫn từ điểm K nằm ngoài đường tròn, ta kẻ tiếp tuyến KA và cát tuyến KCD thì sẽ có:
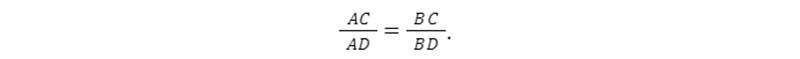
Ta cũng có thêm: Góc KAC = góc ADK, như vậy ta có:
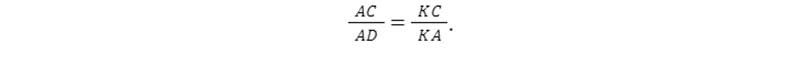
Cách vẽ đường cát tuyến chính xác
Với các thông tin bên trên chắc chắn các bạn đã hiểu được cát tuyến là gì rồi đúng không nào? Do đường cát tuyến có thể cắt được cả đường thẳng, đường tròn và đường cong nên sẽ có cách vẽ khác nhau mà các bạn cần hết sức lưu ý.
Đối với đường tròn và đường cong
Muốn vẽ được đường cát tuyến cho một đường tròn hoặc đường cong bất kỳ rất đơn giản, các bạn chỉ cần làm theo 2 bước dưới đây:
- Bước 1: Xác định chính xác trước 2 điểm bất kỳ phân biệt nằm ở trên đường tròn hoặc đường đường cong đó.
- Bước 2: Dùng bút kẻ một đường thẳng đi qua hai điểm phân biệt đã xác định trước đó. Như vậy là chúng ta đã có ngay 1 đường cát tuyến của đường tròn hoặc đường cong rồi.
Đối với hai đường thẳng
Để vẽ được đường cát tuyến của 2 đường thẳng, các bạn hãy thực hiện theo 2 bước dưới đây:
- Bước 1: Đầu tiên, các bạn cần phải xác định được chính xác 2 điểm bất kỳ thuộc hai đường thẳng đó.
- Bước 2: Sau đó, nhắm thật chuẩn rồi kẻ một đường thẳng đi qua hai điểm đó. Vậy là các bạn cũng đã vẽ được một đường cát tuyến của hai đường thẳng rồi.
Một số dạng bài tập liên quan đến cát tuyến hay có trong bài thi
Để giúp cho các bạn học sinh có hiểu rõ hơn đường cát tuyến là gì, chúng tôi sẽ chia sẻ bài tập liên quan đến mảng kiến thức này cùng lời giải cụ thể để mọi người cùng tham khảo. Cụ thể như sau:
Bài tập 1: Từ một điểm K nằm ở bên ngoài của đường tròn, chúng ta kẻ các tiếp tuyến lần lượt là KA, KB và cát tuyến KCD đến đường tròn (O). Gọi M là giao điểm của 2 đường thẳng OK và AB. Vẽ dây DI đi qua M. Hãy chứng minh rằng:
- KIOD là một hình tứ giác nội tiếp của đường tròn (O).
- KO chính là đường phân giác của góc IKD.
Lời giải
Theo đề bài cho, chúng ta có hình vẽ như sau:
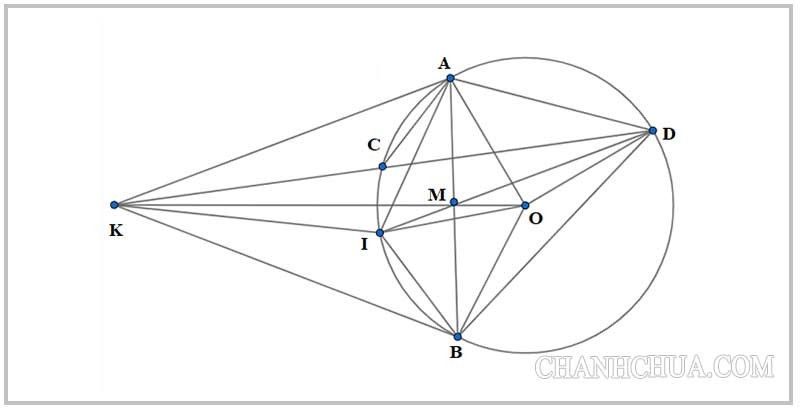
- Ta có: AIBD là tứ giác nội tiếp và AB giao ID tại điểm M
Suy ra: MA. MB = MI.MD
Mặt khác, ta có KAOB cũng là tứ giác nội tiếp nên MA.MB = MO.MK
Như vậy: MI.MD = MO.MK
Vậy KIOD là tứ giác nội tiếp của đường tròn (O)
- Xét đường tròn ngoại tiếp tứ giác KIOD, ta có: OI = OD = R
Suy ra: Góc OKI = góc OKD
Vậy OK chính là đường phân giác của góc IKD.
Bài tập 2: Từ một điểm M cố định ở bên ngoài của đường tròn (O), hãy kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
- Các bạn chứng minh rằng ta luôn có MI² = MA.MB và tích này sẽ không phụ thuộc vào vị trí của cát tuyến MAB
- Khi cho MT = 20cm, MB = 50cm, các bạn hãy tính bán kính của đường tròn?
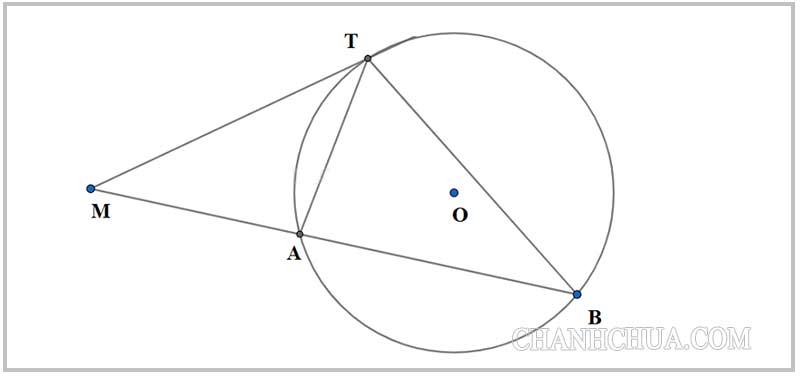
Bài giải
- Ta có:
- Góc M chung.
- Góc B = góc MTA vì cùng chắn cung nhỏ TA.
- Tam giác BMT đồng dạng với tam giác TMA.
Nên suy ra:
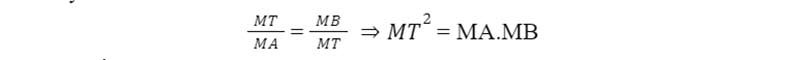
Vì cát tuyến MBA được kẻ tùy ý nên ta có: MT.MT = MA.MB không phụ thuộc vào vị trí của đường cát tuyến MAB.
- Chúng ta gọi bán kính của đường tròn là R. Ta có:
![]()
Thay số vào, ta được:
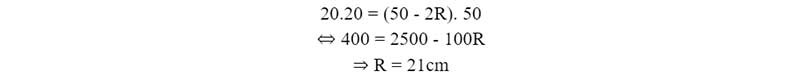
Hy vọng bài viết này mang đến những kiến thức Toán học hữu ích để các bạn nắm được cát tuyến là gì? Cách vẽ và làm bài tập thực hành chính xác. Nếu có thắc mắc gì về nội dung bài viết, hãy bình luận ở bên dưới bài viết để nhận được câu trả lời ưng ý nhất.







