Trực tâm là gì? Cách xác định trực tâm đơn giản nhất
Trực tâm trong không gian hay trực tâm trong tam giác là những kiến thức trong chương trình toán học ở cơ sở mà chúng ta đã được học. Tuy nhiên sau thời gian dài không ôn tập lại nhiều người sẽ không còn nhớ rõ trực tâm là gì. Nếu đang cần lấy lại kiến thức về trực tâm, hoặc những với những bạn chưa học tới kiến thức này nhưng muốn tìm hiểu trước hãy cùng chanhchua.com theo dõi bài viết sau đây nhé.
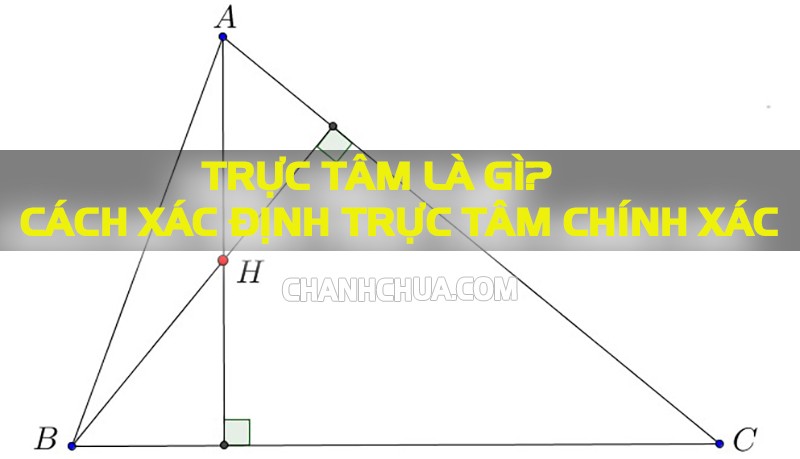
Tìm hiểu trực tâm là gì?
Trong một tam giác, khi 3 đường cao của tam giác đó giao nhau tại một điểm vậy điểm giao đó được gọi là trực tâm. Khi phát biểu các bạn có thể phát biểu đơn giản hơn như sau: “Trực tâm của tam giác chính là giao điểm của 3 đường cao”.
Đường thẳng nối từ đỉnh của một tam giác xuống cạnh đối diện và vuông góc với cạnh đó tại điểm cắt được gọi là đường cao trong tam giác. Cạnh đối diện này còn có thể được gọi là cạnh đấy tương ứng với đường cao của nó. Độ dài đường cao thì theo định nghĩa chính là khoảng cách giữa đỉnh và đáy tương ứng của nó
Ví dụ: Cho tam giác ABC có ba đường cao lần lượt là AK, BN, CQ. Gọi O là giao điểm của ba đường cao trên thì O là trực tâm của tam giác ABC.
Các tính chất của trực tâm trong tam giác
Trực tâm của tam giác có khá nhiều định lý và tính chất quan trọng. Nếu muốn làm tốt những dạng bài tập toán hình học, chắc chắn các bạn phải nắm rõ được các định lý cũng như các tính chất mới có thể vận dụng để làm bài tập hiệu quả và nhanh chóng.
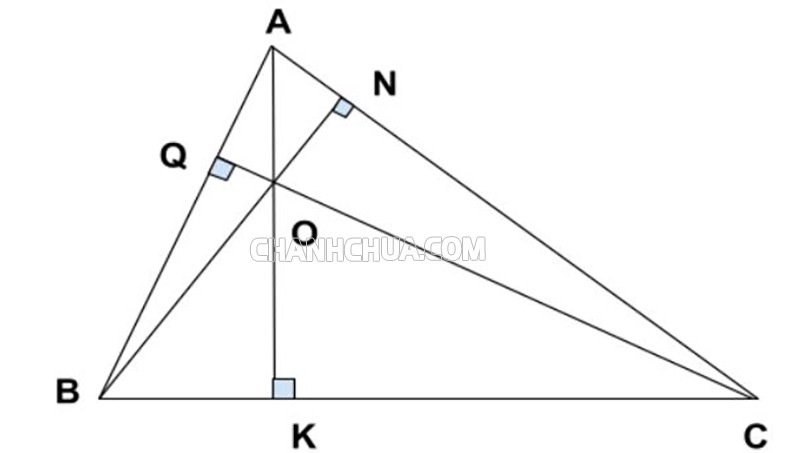
- Nếu ba đường cao của tam giác mà cùng đi qua một điểm thì điểm đó sẽ được gọi là trực tâm của tam giác. Còn khoảng cách từ tâm của đường tròn ngoại tiếp tam giác đến trung điểm của một cạnh sẽ bằng ½ khoảng cách từ trực tâm đến đỉnh còn lại của tam giác đó.
- Trong một tam giác, nếu đường trung tuyến đồng thời đóng vai trò là đường phân giác thì tam giác đó được gọi là tam giác cân.
- Trong một tam giác cân, có đường trung trực ứng với cạnh đáy sẽ đồng thời là đường cao, đường phân giác và cũng là đường trung tuyến của tam giác đó.
- Trong một tam giác đều, trực tâm đồng thời là trọng tâm, là tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp của tam giác đó.
- Định lý Carnot: Đường cao tương ứng với một đỉnh trong một tam giác cắt đường tròn ngoại tiếp tam giác đó ở đâu thì điểm đó chính là điểm đối xứng với trực tâm của tam giác, qua cạnh đáy đối xứng với đỉnh.
Hướng dẫn cách xác định trực tâm của một tam giác đơn giản
Khi xác định trực tâm của một tam giác, các bạn không nhất thiết phải vẽ 3 đường cao, bởi chỉ cần vẽ 2 đường cao trong tam giác là đã có thể xác định được trực tâm.
Đối với các loại tam giác thông thường như tam giác nhọn, tam giác tù hoặc những tam giác đặc biệt như tam giác cân, tam giác đều thì cách xác định trực tâm sẽ là như nhau.
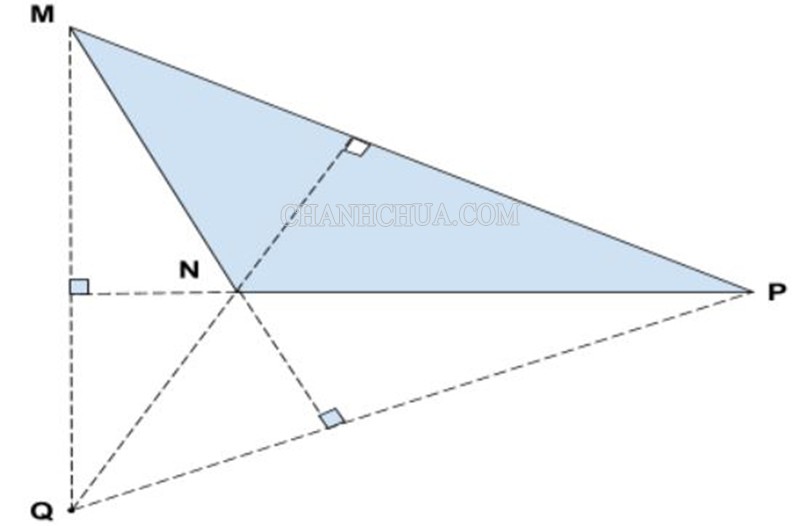
Từ hai đỉnh của tam giác ta sẽ kẻ đường cao tương ứng tới hai cạnh đối diện. Điểm giao nhau của hai đường cao sẽ là trực tâm của tam giác và chắc chắn đường cao còn lại của tam giác cũng sẽ đi qua điểm trục tâm này.
Cách để xác định trực tâm tam giác vuông
Để có thể xác định được trực tâm tam trong giác vuông thì bằng dấu hiệu nhận biết sẽ giúp bạn dễ xác định hơn. Đối với tam giác vuông, trực tâm của nó chính là đỉnh góc vuông của tam giác đó.
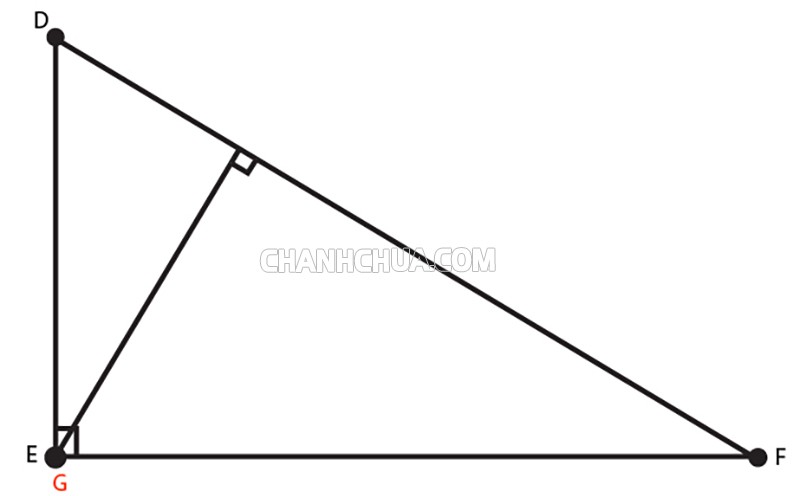
=> G chính là trực tâm của tam giác DEF
Cách để xác định trực tâm trong tam giác có góc tù
Đối với tam giác tù thì trực tâm của nó sẽ nằm ở miền ngoài tam giác đó.
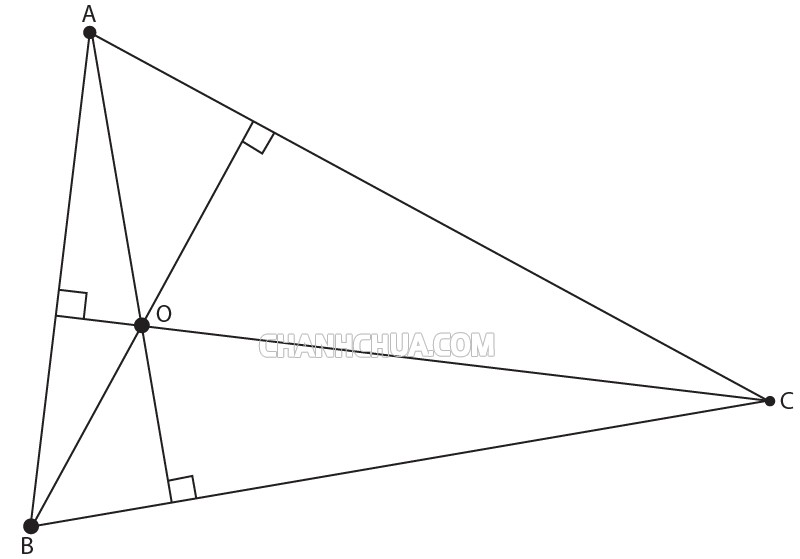
=> O là trực tâm giác ABC
Cách để xác định trực tâm trong tam nhọn
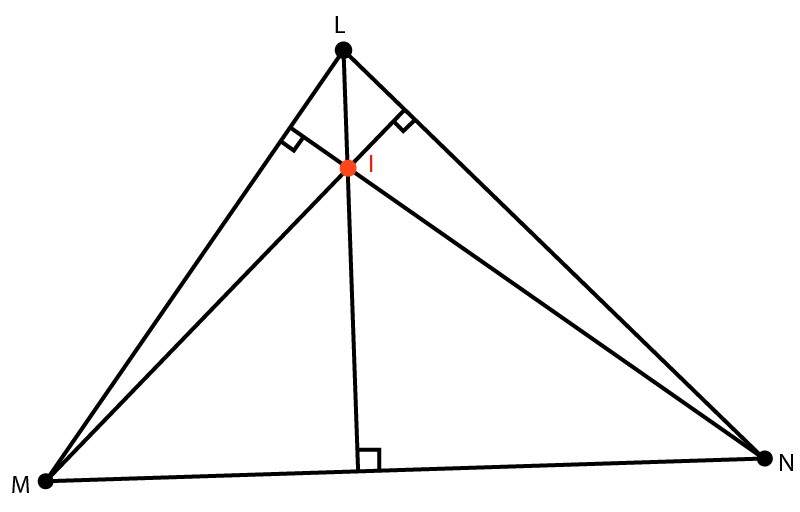
Đối với tam giác nhọn, trực tâm của nó sẽ nằm ở miền trong tam giác đó.
=> I là trực tâm tam giác LMN
Trên đây chúng tôi và các bạn vừa cùng nhau tìm hiểu về chủ đề “Trực tâm là gì? Cách xác định trực tâm đơn giản”. Hy vọng, qua những thông tin chúng tôi chia sẻ trong bài sẽ giúp các bạn nắm vững hơn kiến thức về trực tâm để áp dụng tốt nhất trong bài bài toán hình học!







